Природа человеческого сознания устроена так, что всякие новые идеи воспринимаются им намного лучше, если сопровождаются поясняющими суть картинками. Именно поэтому, как хорошо известно психологам, математикам и физикам, практически любую научную концепцию легче объяснить или постичь, если она изложена не алгебраическим языком формул и уравнений, а графическими средствами схем, диаграмм и визуальных моделей. Иначе говоря, языком геометрии.

В гигантском инструментарии современной геометрии имеется один весьма специфический раздел, именуемый топологией. В отличие от других разделов, где большое значение имеют соотнесения длин, площадей, углов и других количественных характеристик объектов, топологию это все не интересует, поскольку здесь изучаются иные, качественного свойства вопросы о геометрических структурах. В топологии не спрашивают, насколько велика или мала данная вещь, ибо любой объект здесь можно как угодно сжимать и растягивать при условии сохранения целостности, то есть без разрывов и склеек. По этой причине топологию иногда называют резиновой геометрией.

Что же касается вопросов качественного свойства, составляющих суть топологии, то они обычно сводятся к тому, как связаны друг с другом элементы объекта. Типичные вопросы выглядят примерно так. Можно ли вещь разделить на отдельные части? Сколько у объекта поверхностей? Есть ли там дырки, а если есть, то сколько? Глубокая связь между столь абстрактными, на первый взгляд, проблемами топологии и физическими свойствами конкретных объектов природы далеко не всегда самоочевидна. Скорее даже наоборот, для многих людей топология представляется наукой, весьма далекой от физики реального мира, где невозможно как угодно растягивать и сжимать вещи, не нарушая их целостность.

Прежде, чем переходить к иллюстрациям, демонстрирующим огромную важность топологии для физики, уместно привести какой-нибудь простой жизненный пример, поясняющий суть топологических подходов к анализу качественных проблем геометрии. Нередко в качестве такого примера привлекают карту метрополитена крупного города вроде, скажем, Москвы. Карта метро не дает сколь-нибудь содержательной информации о том, как далеко станция «Парк Горького», находящаяся в южном сегменте кольцевой линии, расположена от станции «Ботанический сад» на радиальной линии северного направления. Масштаб расстояний между пунктами не выдерживается, более того, тут даже не соблюдаются направления по сторонам света при движении от одной точки к другой. Однако карта эта достоверно рассказывает обо всех линиях и станциях, а также об узлах (станциях пересадок), соединяющих все линии метрополитена в целое и действительно существенных при движении из одного пункта в другой. Так, от «Парка Горького» до «Ботанического сада» можно добираться через много станций по кольцевой линии, а можно и короче по радиусу, сделав пересадку в Центре. Иначе говоря, карта метро дает не столько геометрическую, сколько топологическую информацию.

*

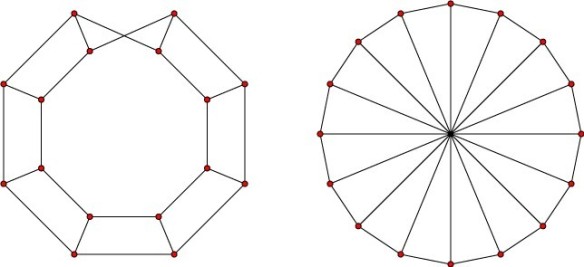
Похожим по форме и более актуальным здесь по сути примером можно считать объект теории графов, именуемый лестница Мебиуса [1]. Этот граф, всегда имеющий четное число узлов-вершин, попарно соединенных ребрами-«перекладинами», своим видом напоминает бесконечную лестницу, у которой начало и конец замкнуты с полупереворотом на 180 градусов. Иначе говоря, это простейший аналог ленты Мебиуса, составленный из одномерных отрезков линий. И если полагать, что лента Мебиуса – как элементарный образец односторонней поверхности – лежит в основе геометрии вселенной, то лестница Мебиуса оказывается очень удобной моделью для демонстрации принципиально важных топологических моментов в устройстве этой конструкции.

Два эквивалентных представления лестницы Мебиуса

Легко увидеть, что все точки лестницы лежат на одной замкнутой линии. Если эту линию, пользуясь резиновыми возможностями топологии, развернуть из формы двойного кольца и равномерно натянуть на окружность, то получится другое эквивалентное представление лестницы Мебиуса. Из которого ясно видно, что точки-узлы каждой пары симметрично расположены в противоположных концах этой вселенной, а соединяющая их перекладина проходит через центр окружности. Хотя это очевидно из самой иллюстрации, имеет смысл подчеркнуть, что в центре данной конструкции никакого узла нет, но геометрически он важен как единая точка схождения всех перекладин-диаметров при симметричном распределении узлов по окружности. Это, можно сказать, самая простая и наглядная демонстрация базовой идеи, согласно которой каждый протон в одной точке пространства является электроном в противоположном конце вселенной. Причем всякий раз, когда электрон и протон каждой пары с гигантской частотой меняются своими местами, то происходит это через пустоту геометрического центра.

Кроме того, характерную топологию лестницы Мебиуса несложно углядеть в общеизвестной структуре молекул ДНК. Понятно, наверное, что было бы легкомыслием отнестись к этому совпадению как к случайности. Но для более тщательного разбора взаимосвязей между строением вселенной, биологией и сохранением информации будут отведены отдельные разделы в дальнейшем.

Здесь же разворачиваются Вторые Картезианские игры, посвященные стыкам физики и геометрии. Причем, как это следует из их названия, главный упор Игр должен делаться на ключевую декартову идею об основополагающей роли вихрей в устройстве мироздания. С точки зрения топологии, надо отметить, эта пафосная идея выглядит вполне естественной, поскольку разного рода вихри теснейшим образом связаны с понятием «топологический дефект». А топологические дефекты на сегодняшний день считаются наиболее перспективным путем к постижению того, как в этом мире из ничего появляется что-то (и все-все-все остальное в придачу).

**

Для пояснения сути термина топологический дефект в самых общих чертах, полезно привлечь идею симметрии. И зафиксировать, что наиболее симметричным во всех отношениях объектом или пространством считается среда, напрочь лишенная каких-либо свойств и отличий во всех своих местах и направлениях. Иначе говоря, всюду безвидная. Тогда любая деталь или особенность, появляющаяся в повсюду одинаковой среде называется нарушением симметрии, а если же это нарушение способно сохранять стабильность, то оно именуется топологическим дефектом или, иначе, топологическим солитоном. Как показывают эксперименты и подтверждают теоретические расчеты, топологические дефекты обычно являются разновидностями вихревого движения: вихревыми кольцами, вихревыми нитями, конвекционными ячейками в жидкостях и газах; винтовыми дислокациями в кристаллах, вихревыми решетками в сверхтекучих или сверхпроводящих материалах, и так далее.

До геометрической роли конвекционных ячеек, вихревых нитей и винтовых дислокаций Игры доберутся естественным образом, а пока речь пойдет о торе – одной из самых важных в топологии фигур, имеющей форму вихревого кольца или, скажем, надутой автомобильной камеры. Между графом лестницы Мебиуса и тором просматривается достаточно очевидное родство, если заметить, что тор является поверхностью вращения для ленты Мебиуса – если ее вращать вокруг осевой линии. Богатые топологические свойства тора интересны во множестве физических аспектов, но сейчас имеет смысл задержать внимание на одном, связанном с так называемой проблемой причесывания поверхности.

Эта проблема, к примеру, чрезвычайно актуальна при выборе правильной формы для реактора термоядерного синтеза, где облако плазмы необходимо удерживать в заданном ограниченном объеме с помощью магнитного поля. Чтобы понять суть задачи, надо представить себе замкнутое пространство формы, окружающей плазму. В каждой точке поверхности этого пространства компонент магнитного поля, параллельный поверхности формы, должен быть ненулевым, а иначе плазма даст в этом месте утечку и удержать ее не удастся. Переформулировав суть чуть иными словами, можно сказать, что вектор магнитного поля в каждой точке поверхности подобен растущему здесь волосу, а задача отыскания поля нужной формы эквивалентна задаче такого причесывания поверхности, чтобы все-все волоски были уложены горизонтально.

Оказывается, что существование решения для этой проблемы зависит исключительно от топологической природы выбранной поверхности. Если, например, в качестве поверхности выбрана сфера – то решения у задачи просто не существует. Иначе говоря, покрытый шерстью шар полностью причесать невозможно, а значит магнитное удержание шара плазмы организовать не удастся в принципе. (Любопытным следствием проблемы с причесыванием оказывается то, что в любой момент времени в какой-то из точек на поверхности Земли непременно стоит безветренная погода.) Единственный же тип поверхности, для которого «гладкая прическа» возможна – это форма вихревого кольца, то есть тор. По этой причине тороидальной формы магнитное поле и стало решением, повсеместно используемым в конструкциях экспериментальных термоядерных реакторов.

***

В примере с задачей удержания плазмы несложно углядеть аналогию с другой, куда более масштабной проблемой. А именно, с поиском оптимальной формы для мембраны, образующей пространство 3-мерной вселенной, известной человеку. В общих чертах уже понятно, что это должно напоминать тор. Но только не обычный тор, просто похожий на надутую автомобильную камеру, а довольно особенный.

Во-первых, топологически эта конструкция непременно должна иметь свойства односторонней поверхности. Самым простым трехмерным вариантом ленты Мебиуса без краев, взаимопересечений и склеек является, как известно, поверхность Клейна, более известная как бутылка Клейна.

Во-вторых, пространство вселенной является ориентируемым, то есть здесь наблюдаются вполне очевидные различия между правым и левым. Всякая же односторонняя поверхность по природе своей является неориентируемой. Простейший трюк, с помощью которого лента Мебиуса превращается в ориентируемую поверхность, – это двухслойный вариант той же самой конструкции. Строго говоря, такая поверхность уже не является односторонней, однако важнейшие свойства ограниченного и замкнутого на себя бесконечного пространства здесь сохранены. Следовательно, форму вселенной логично представлять как двухслойную бутылку Клейна.

И в-третьих, наконец, каким-то образом топология космоса одновременно должна быть похожа на мяч, сшитый из 12 пятиугольных кусков кожи. Не столько потому, что эта форма упоминается в трудах древнего мудреца Платона, но по той причине, что совсем недавно эта же топология футбольного мяча была «переоткрыта» в карте фонового космического излучения от спутника WMAP – как додекаэдрическое пространство Пуанкаре.

[1] Richard K.Guy, Frank Harary. «On the Möbius ladders». Canad. Math. Bull. 10: 493-496 (1967)