Большой комплекс взаимосвязанных задач, совокупно известных под названием Langlands Program, иногда также называют «Теорией великого объединения математики». Иначе говоря, множеством ученых из разных стран мира на протяжении вот уже почти полувека предпринимаются очень серьезные усилия ради грандиозной общей цели.

Понемногу, шаг за шагом им удается показать, что необъятный мир математических исследований, когда-то представлявшийся совокупностью самых разных и зачастую никак не связанных между собой территорий, на самом деле устроен в корне иначе. То есть области, которые прежде воспринимались как не имеющие ничего общего друг с другом, в действительности оказываются эквивалентными описаниями одной и той же в сущности структуры.

Структуры, одновременно и чрезвычайно сложной в освоении, и – как многие предчувствуют – элегантно простой и красивой в своей итоговой картине. Короче, единой конструкции в основе всей математики – наверняка прекрасной, но по сию пору наукой еще не постигнутой.

И при этом – что удивительно – на просторах всенародной энциклопедии «Википедия», где число статей лишь в одном русскоязычном разделе уже приближается к миллиону, на русском языке нет об этом практически никакой информации.

То есть нет там ни собственно статьи «Программа Ленглендса» (именно в таком написании термин закрепился в отечественной науке), ни статьи «Роберт Лэнглендс» (более корректное, пожалуй, произношение фамилии) – об известном канадском математике, запустившем все это дело еще в 1960-е годы, а в минувшем октябре отметившем свое 76-летие.

Столь откровенное безразличие общества к большим свершениям, происходящим на передовых рубежах теоретической науки, характерно, конечно, не только для нашей страны. Это явление, если присмотреться, ныне фактически повсеместное.

Ученых, ясное дело, такая тенденция всерьез беспокоит. Именно по этой причине, собственно, в городе Торонто, Канада, в октябре нынешнего года был устроен первый международный Симпозиум Филдсовской медали, нацеленный на более широкую популяризацию достижений математической науки в народных массах.

Отныне это мероприятие планируется Институтом Филдса проводить ежегодно, причем каждый очередной симпозиум – как и первый – мыслится сфокусированным на такой области математики, где достигнуты выдающиеся успехи одним из недавних лауреатов Медали Филдса. (На всякий случай, если кто не в курсе, Филдсовская медаль считается своего рода «математическим аналогом» Нобелевской премии – высшей среди математиков наградой, которой раз в 4 года награждаются ученые в возрасте не более 40 лет.)

Что же касается тематической направленности Первого филдсовского симпозиума, то конечно же совсем не случайно он был посвящен «Фундаментальным основам Программы Ленглендса». А в качестве «главного героя» форума был выбран первый великий математик вьетнамского народа Нго Бао Тяу, в 2008 году удостоенный медали Филдса за доказательство Фундаментальной леммы в теории Ленглендса (сформулированного еще в 1983 году важного, но технически вспомогательного утверждения, которое, однако, никому не удавалось доказать на протяжении четверти века; Нго Бао Тяу не только доказал лемму неожиданным и новаторским образом, но и открыл попутно множество неведомых прежде взаимосвязей).

Чтобы стало понятнее, почему все это действительно важно не только для узко специализированных теоретиков, глубоко погрузившихся в свои математические абстракции, но и в целом для человечества, правильнее всего предоставить слово специалисту. Который не только в деталях понимает предмет, но и достаточно внятно может объяснить суть открытий обычным людям, далеким от математики.

В данном случае на эту роль практически идеально подходит Эдвард Френкель, профессор математики из Калифорнийского университета Беркли и один из главных научных организаторов первого Симпозиума Филдсовской медали. В большом интервью, предшествовавшем мероприятию, Френкель дал популярный обзор Программы Ленглендса, ее общей истории и нынешних особенностей.

Целиком оригинал этого интервью можно найти на сайте Университета Торонто, ну а в сокращенном вольном пересказе по-русски тезисы Френкеля выглядят примерно так.

Что рассказал профессор Френкель

Исследования, ведущиеся в рамках Программы Ленглендса, нередко пытаются охарактеризовать как строгую разработку математического языка, устанавливающего соответствие между теорией чисел и математическим анализом. Хотя можно сказать и так, однако в действительности это много-много больше.

Когда в конце 1960-х годов Роберт Лэнглендс затевал свою Программу, то главным стимулом, подтолкнувшим его к этим изысканиям, были весьма трудные в своем решении вопросы из области теории чисел.

В этой области часто приходится иметь дело с решениями степенных алгебраических уравнений (типа, скажем, y² = x³ + 5x +3), но с той особенностью, что все вычисления здесь ведутся лишь над целыми числами «по модулю p». Принципы модульной арифметики проще всего пояснить циферблатом часов, на котором сколько бы времени не прошло, показания стрелок всегда приведены «по модулю 12» (правда, при более строгом подходе к делу на циферблате следовало бы писать цифры от 0 до 11, но это уже технические нюансы).

В теории же чисел по ряду принципиальных причин особо важны ситуации, когда числовые наборы, задающие множество значений уравнения, формируются по таким модулям p, которые являются простыми числами (делящимися лишь на себя и 1). И в этих условиях, когда аналитик сталкивается с тем или иным уравнением, крайне желательно бывает заранее знать, сколько именно решений имеет данное уравнение по модулю p – для всех возможных значений простого числа p. Так вот оказывается, что это чрезвычайно сложный вопрос.

Глубокое и неожиданное прозрение Лэнглендса заключалось в том, что неведомые числа решений можно, как оказалось, считывать с объектов из совершенно другой области математики, именуемой «гармонический анализ».

Данный раздел математического анализа занимается изучением функций особенного рода – имеющих прямое отношение к регулярным колебаниям и к музыке, а потому называемых гармоническими. Для простейшего примера, все знают базовые тригонометрические функции, такие как sin(x) и cos(x). К этому же элементарному ряду принадлежат также функции sin(nx) и cos(nx) при всех целочисленных значениях n.

Согласно результатам, полученным еще Жаном Батистом Фурье в начале XIX века, почти все функции, являющиеся периодическими, можно эквивалентно записать в виде «суперпозиции» или композиции из этих простейших базовых функций. Это очень сильное и, как показала жизнь, чрезвычайно полезное утверждение!

В приложении к области коммуникаций, скажем, представьте, что у вас есть сигнал, описываемый некоторой функцией. Преобразование ее к виду суммы из простых тригонометрических функций представляет собой декомпозицию – или разложение – сигнала на «элементарные гармоники» (систематически обрабатывать которые всегда несоизмеримо проще).

Это, собственно, и есть то, в чем заключается суть гармонического анализа: отыскание неких элементарных гармоник, вроде sin(nx) и cos(nx), но только в намного более общей ситуации, а также отыскание путей к разложению произвольных функций в терминах таких гармоник.

Это замечательная теория, находящая ныне огромное множество всевозможных полезных приложений. Но следует, однако, подчеркнуть, что поначалу она выглядела чрезвычайно далекой от теории чисел.

И вот тут-то и случился сюрприз. Роберт Лэнглендс предположил и в общих чертах показал, что эти два мира – теория чисел и гармонический анализ – неразрывно связаны друг с другом.

Выражаясь более аккуратно, он предположил, что вопросы в теории чисел, вроде отыскания числа решений для уравнений по простому модулю, могут быть решены с помощью аппарата гармонического анализа.

В частности, для всякого уравнения, типа приведенного выше, существует некоторая гармоническая функция, которая как бы заранее уже все «знает» о числах решений этого уравнения по всем простым модулям (то есть позволяет достаточно просто их вычислять).

Поскольку это взаимное соответствие ниоткуда не следовало, то выглядело данное открытие крайне озадачивающе – словно какая-то магия и волшебство…

Именно по этой причине, собственно, математический мир и был столь сильно взволнован программой Ленглендса. Прежде всего потому, что развитие этого направления дает нам способ решать такие задачи, которые прежде выглядели как неразрешимые проблемы.

Есть тут и второй, не менее важный аспект. Программа Ленглендса указывает на какие-то очень глубокие и фундаментальные взаимосвязи между разными областями математики.

Конечно же, очень хочется узнать, что же действительно здесь происходит. Почему эти вещи связаны вот таким образом? Но пока еще все мы полностью этого так и не понимаем…

Примерно так выглядело происхождение программы Ленглендса.

Ну а затем стало происходить вот что. Те же самые загадочные паттерны и соответствия начали постепенно обнаруживаться не только в других областях математики, вроде геометрии, но также и в квантовой физике.

Программу Ленглендса не просто так порою называют Теорией великого объединения математики. Эта Программа указывает на некие всеобщие, универсальные феномены и взаимосвязи между этими феноменами, накрывающие самые разные области математики. Именно здесь, быть может, и содержатся ключи к пониманию того, что же вообще представляет собой математика…

На сегодняшний день программа Ленглендса – это гигантская территория исследований. Поскольку идеи Программы распространились во множестве направлений, сейчас здесь работает большое сообщество специалистов из весьма разнообразных областей математики и теоретической физики.

Ситуация выглядит так, словно у вас имеется множество совершенно разных языков, а также наборы предложений из этих разных языков, про которые вам уже известно, что они означают одну и ту же вещь. И вот вы раскладываете эти предложения рядом друг с другом, и мало-помалу начинаете нарабатывать словарь, который позволяет вам переводить одни и те же, по сути, утверждения, но только сформулированные в разных областях математики, в квантовой теории поля или в теории струн.

Работы над Программой Ленглендса, конечно же, будут продолжаться и дальше. В завершение интервью Эдвард Френкель сказал об этом так:

Чем больше мы узнаем, тем больше мы понимаем, насколько мало мы в действительности знаем. Как я уже говорил, красота Программы Ленглендса в том, что она указывает на загадочные связи между разными областями математики.

И самый большой из вопросов, на мой взгляд, такой: почему эти взаимосвязи существуют, каков стоящий за ними механизм? Мы все еще этого не знаем, но мы над этим работаем.

Теперь мы уже лучше понимаем, каким образом различные куски паззла прикладываются друг к другу.

Но нам нужны новые свежие идеи.

Ну а пока новых и свежих идей на горизонте не появилось, имеет, быть может, смысл повнимательнее оглядеться вокруг. И присмотреться к идеям достаточно старым, но только как следует все еще не разработанным.

Две тайны или одна?

Среди великого множества все еще не разрешенных человеком загадок природы две тайны особо впечатляют своими масштабами, а потому и вспоминаются чаще других.

Загадка первая, наиболее дискомфортная: что представляют собой темная материя и темная энергия, на которые приходится 96% вселенной?

Вершина современных научных знаний о природе мироздания, Стандартная Модель физики, содержательно описывает наблюдаемый мир в терминах кварков, лептонов и прочих квантовых частиц-полей, переносящих взаимодействия. Однако приходится признать, что все эти вещи составляют всего лишь 4% от общей массы-энергии вселенной.

Про остальные 96% наука не знает и не может сказать ничего. Кроме как называть неведомое «темной материей» и «темной энергией».

Загадка вторая – это тайна «непостижимой эффективности математики» (как сформулировал ее в свое время Юджин Вигнер).

На протяжении всей истории науки ученые постоянно сталкиваются с ситуациями, когда математические уравнения, выводимые ими для описания физических закономерностей, в действительности «знают» больше, чем записавшие их первооткрыватели.

Типичный пример. Когда, скажем, Альберт Эйнштейн завершил в 1916 году разработку своей общей теории относительности, то при размышлениях над выведенными уравнениями он вдруг обнаружил в них совершенно неожиданное послание, сообщавшее, что вселенная расширяется.

Эйнштейн же в то время был уверен в картине стационарного и неподвижного мироздания, поэтому не поверил, что физическая вселенная способна сжиматься или расти в размерах. Иначе говоря, он проигнорировал то, о чем говорили ему уравнения. Спустя еще 13 лет астрономические наблюдения Эдвина Хаббла продемонстрировали убедительные свидетельства расширению вселенной. А Эйнштейн, соответственно, упустил возможность сделать одно из наиболее эффектных и неожиданных научных предсказаний в истории науки.

Сам собой возникает интересный вопрос: каким образом эйнштейновы уравнения «знали» что вселенная расширяется, когда сам он этого не знал и знать не хотел?

И если математика, как некоторые полагают, это не более чем язык, который человек придумал и использует для описания мира (то есть лишь изобретение человеческого мозга), то как же она может выдавать нечто такое, что находится явно за пределами вкладываемого туда людьми?

Всякий раз, когда уравнения математики сами «знают» и дают ученым предсказания о еще не открытых частицах и о любых других свойствах физической реальности, на ум невольно приходит странноватая идея примерно следующего типа: «Быть может, это так по той причине, что математика и есть реальность» (пользуясь выражением Брайена Грина, известного популяризатора струнной теории и профессора физики из Колумбийского университета).

Но отсюда возникает следующий большой вопрос: почему же тогда вселенная сделана только лишь из небольшой части всей доступной человеку математики?

Еще раз цитируя Брайена Грина: «Математики имеется очень много. Лишь совсем тоненький ее слой имеет сегодня реализацию в физическом мире. Снимите с полки любую математическую книгу и вы увидите, что большинство уравнений в ней не соответствует никакому физическому объекту или физическому процессу»…

Очередной подходящей цитаты от какого-нибудь знаменитого научного светила под рукой не находится, однако следующая логичная идея лежит, по сути, на поверхности. А значит, ее наверняка кто-то из авторитетов уже озвучивал (и даже если нет, это ничего не меняет):

Если наблюдаемый человеком мир составляет лишь крошечную, 4-процентную долю от всего, что есть во вселенной, а из того гигантского комплекса математики, что уже освоен человеком, лишь крошечная доля отвечает за описание наблюдаемой реальности, то, быть может, ответ на две большие загадки природы уже нами найден?

То есть не исключено, что математики и теоретики математической физики, давно и подробно исследующие абстрактные миры, местами или даже полностью оторванные от реальности, на самом деле изучают те самые 96% невидимой для человека вселенной…

Доказать подобную гипотезу, конечно, пока что нет никакой возможности. Однако для ее подкрепления полезно напомнить еще одну, третью, великую загадку, без которой общая картина «не имеет смысла» – в буквальном понимании этих слов.

Что нарисовал профессор Пенроуз

В 2004 году у известного британского физика и математика Роджера Пенроуза вышла в свет толстенная монография «Путь к реальности, или полный путеводитель по законам, управляющим Вселенной» (Roger Penrose, «The Road to Reality. A Complete Guide to the Laws of the Universe». Jonathan Cape, 2004. Имеется русский перевод от ижевского издательства НИЦ «Регулярная и хаотическая динамика», 2007).

Так вот, в этой книге целый самостоятельный подраздел (1.4) посвящен еще одной великой тайне – о том непостижимом положении, которое занимает человеческое сознание между физической реальностью и миром математики.

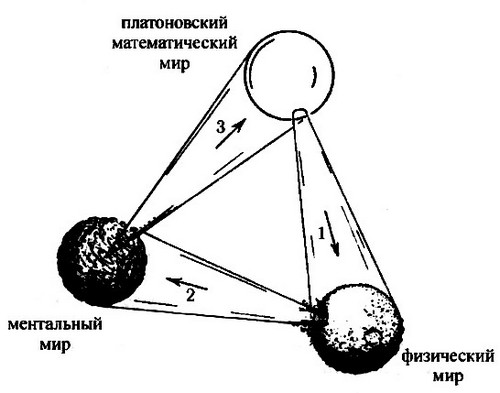
Пенроуз называет этот комплекс «три мира или три формы существования»: форма физического существования, форма ментального существования и форма математического существования (платоновский мир идей). Понятно, что все эти формы тесно друг с другом связаны, «причем соответствующие связи настолько же фундаментальны, насколько и загадочны» (цитируя автора).

С помощью вот такого рисунка Пенроуз схематически изобразил все эти три формы существования в виде сфер, представляющих собой объекты, принадлежащие трем различным мирам. Здесь же показана и суть загадочных связей между этими мирами.

Суть загадок достаточно ясна. Как уже отмечалось выше, если рассматривать сферу математики, то непосредственное отношение к процессам физического мира имеет лишь некая совсем малая часть мира математического.

Аналогично, в сфере мира физического (насколько это известно современной науке) лишь очень-очень небольшая часть имеет отношение к сознанию и связана с феноменом ментальной деятельности.

И наконец, третья взаимосвязь-загадка, связывающая сознание со сферой математики, также вполне очевидна: размышления человека об абсолютных математических истинах составляют чрезвычайно малую долю от нашей совокупной мыслительной деятельности.

В итоге же из этих достаточно очевидных соотношений складывается явный парадокс – когда каждый мир заключает в себе в качестве малого фрагмента весь следующий мир целиком. Но цепочка взаимосвязей при этом замкнута…

Автор честно признает, что не в силах решить эту тройственную головоломку. Но, добавляет он, вместо решения можно продемонстрировать наличие еще одной, даже более головоломной идеи-загадки, превосходящей и перекрывающей все те, на которые уже указано:

Возможно, что все три мира в некотором смысле вовсе не являются отдельными сущностями, но лишь отражают различные аспекты некоей одной, более фундаментальной истины, описывающей мир, как целое. Истины, о которой в настоящее время мы не имеем ни малейшего представления.

Так, подчеркнем, видит ситуацию известный ученый Роджер Пенроуз.

Однако есть и другие известные ученые, имеющие на данный счет вполне определенные идеи и представления. И что самое приятное, эти разные идеи довольно неплохо друг с другом сочетаются.

Но это уже тема для следующего текста.